海报作者：JAMES WEEDON & BOB DOUMA

中文翻译：Zishen Wang （王子申）

This post is also available in English

请设想一下这个场景：你正在一个重要的国际会议上汇报一个激动人心的成果。秉承一向对统计学理论和方法的严谨态度，你对所有的数据都做了统计学检验并给出了置信区间。这些统计分析结果并不只包含P值！你提供的一些数据涉及在不同处理下食草昆虫破坏的叶面积比例。当你准时完成报告时，一位同行问道：“你对破坏比例估计的置信区间是-0.3到0.5，该怎么解释叶面积出现的负值呢？”

观众席里有人笑了。你满脸通红地翻到被提问到的这张幻灯片，嘟囔着给大家解释置信区间和点估计之间的区别。观众们开始小声嘀咕，你好像听到不远处有一只狗在叫。

你该怎么避免这种尴尬又让大家疑惑的情况呢？

生态学和进化学中的比例数据

生态学家和进化生物学家会经常测定许多定量数据，为了方便展示，他们通常会把这些数据表示为比例。许多情况下，这些比例是由计数得来的。在一种情况下，这些比例数据是基于可划分为两个或者更多类别的离散实体的：成功或失败，男性或女性，侵入性或非侵入性。比例数据也可以针对连续型变量：动物进行不同活动的比例；植被调查样本中一种植物功能类型的百分比覆盖率；植物生物量在各个器官和组织上的分配比例。这些比例数据的共同点是只能在0到1之间取值。小于0或大于1的值没有意义。

如果您使用常规统计工具来分析此类数据，可能会导致一些问题。线性回归，方差分析等方法假设因变量可以用正态分布建模。正态分布包含从负无穷大到正无穷大的值，因此不太适合模拟比例数据。用正态分布得出的预测值和置信区间很可能包含比例数据定义区间外的值。此外，残差与预测值有很强的相关性。这些现象都表明，选择错误的模型，会导致不准确的统计推断。

为比例数据构建模型

当比例数据由计数产生时，逻辑回归模型和其扩展型是适当的模型。针对这类成熟的方法，大多数入门的统计学教科书都进行了介绍。

而当比例数据由连续测量产生（例如，植被覆盖百分比，动物行为时间比例，生物量分配比例）时，目前还没有很成熟的方法。常用的解决方案是对数据进行变换，将数据从0到一个区间映射到整个实数行。进行该变换后，可以用一系列包含正态性假设的统计学模型对数据进行处理。反正弦转换通常使用得较多，但David Warton和Francis Hui的分析表明，logit转换效果更好。

近年来，已经有了不使用这种变换的方法。这些方法使用的是从0到某个区间的概率分布。当比例数据是由连续测量，而非计数产生时，可以选择β和Dirichlet分布对其进行分析。

尽管β and Dirichlet回归在十多年前就已经引入，但生态学家和进化生物学家却很少使用它们。由于生态学中高达15%的论文涉及到特定的比例数据，这种对关键方法的长期忽视确实令人感到惊讶。在‘Analysing continuous proportions in ecology and evolution: A practical introduction to beta and Dirichlet regression’中，我们为有兴趣将这些方法应用于数据分析的生态学家和进化生物学家提供了参考。这篇综述可以为那些为无法深入归纳总结这两种方法的研究者提供一定的帮助。

使用β和Dirichlet回归，可以在比例数据原有的尺度上，使用连续或者分类变量，对其进行模拟。β回归适用于单个比例，而Dirichlet回归适用于两个以上的比例，例如，当模拟将植物生物量分配到不同的器官时，Dirichlet回归更为适用。 如果要分析叶片损伤比例，则β回归是更好的选择。

针对分层数据结构和不确定扩散，可以使用β和Dirichlet回归的扩展方法。使用这些方法，可以对数据进行常规的统计分析，例如（多元）线性回归，方差分析（ANOVA）, 协方差分析（ANCOVA），混合效应分析。同时，这些方法也考虑到了比例数据的一些特殊属性。

如果读者熟悉广义线性模型（GLM），那么也可以很好地理解β和Dirichlet回归模型。在这类模型里，预测变量与响应分布参数之间的关系是通过一个链接函数来定义的，通过这种方法可以确保所有预测值都有意义。

在下图中，可以看到，分析比例数据（0到1之间）和预测变量时，正态线性回归（左）和β回归（右）的主要差异。数据显示为蓝色点。每种方法的最佳拟合线是红色虚线。预测变量的一系列值的预测分布为灰色曲线。

很明显，β回归为这些数据拟合了更优的模型，因为预测值和相关分布都落在0和1之间。而正态线性回归的预测值出现了大于1或者小于0的情况，这在分析比例数据时是没有意义的。

针对更复杂的数据，需要使用Dirichlet回归。以下数据来自一项分析不同营养方案下两种植物的生物量分配情况的研究（参见后续的分析）。鉴于每种植物形态和尺寸可能有较大差异，将生物量分配标准化为总生物量的比例便于比较。由于各个器官生物量分配比例的和必须等于1，因此各部分的比例之间存在复杂的相关性。Dirichlet回归解释了这种相关性。

该实例展示了两种植物（Holcus lanatus和Deschampsia flexuosa）的叶片（LMF），根（RMF）和茎（SMF）随时间的生物量分配。对它们进行两种营养处理（低氮和高氮）。黑色线表示模型的预测值。对于一种植物x 营养处理的组合，各个器官的生物量分配比例相加等于1。如果采用除Dirichlet回归以外的其他方法，可能会模拟出超过100%的生物量分配给叶片的情况。

生态学和进化生物学中比例数据分析指南

‘Analysing continuous proportions in ecology and evolution: A practical introduction to beta and Dirichlet regression’旨在为生态学和进化生物学的从业者提供上述分析方法的非技术性介绍。我们着重地介绍了如何将这些方法运用到实际问题上来，而对方法背后的细节原理不做过多阐释。我们考虑到了不同类型的比例数据并提供了与之对应的决策方案，以便使用者将他们的数据和实验设计与正确的分析方法相匹配。

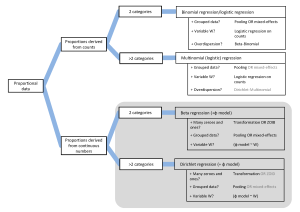
我们提供了β和Dirichlet回归的非技术性描述，并引用了它们在生态学和进化生物学研究中的应用实例。我们还阐述了生态学和进化生物学中所使用数据类型的最重要的扩展（包括分层（嵌套）数据和零膨胀）。

我们提供了三个详细的研究案例。针对所有的案例，我们都提供了数据和R语言代码，以方便读者自行使用。同时为了让读者能够将代码用于自己的研究数据，我们也提供了一些示例代码，这些代码包括R语言中的betareg，DirichletReg，brms和zoib等数据包.

比例数据在生态学和进化生物学中很普遍，需要运用一些特殊的方法来对其进行分析。我们希望这篇文章能够在读者使用β和Dirichlet回归时，给他们提供信息和灵感。

要找到关于β和Dirichlet回归的更多信息，请阅读我们发表在Methods in Ecology and Evolution上的文章“Analysing continuous proportions in ecology and evolution: A practical introduction to beta and Dirichlet regression’